https://arxiv.org/pdf/1409.4842.pdf

1.Introduction
지난 3년간, 딥러닝의 발전으로 인해, 이미지 인식과 물체 검출의 성능은 극적으로 성장하고 있다. 더 좋은 소식은, 이런 성장은 하드웨어의 발전, 데이터 수의 증가, 모델 크기의 확장 등이 아니라, 새로운 아이디어와 알고리즘과 향상된 신경망 구조 덕분이라는 것이다. 2012년에 비해 데이터셋 크기는 달라지지 않았지만, 우리의 GoogLeNet은 12배 적은 파라미터로 더 정확한 결과를 얻었다. 물체 검출에서 가장 큰 소득은 딥러닝을 사용하거나 더 큰 모델을 사용한 것이 아닌, R-CNN처럼 딥러닝 구조와 기존 컴퓨터 비전 알고리즘의 시너지에서 얻어졌다.
파워와 메모리 사용 면에서 우리 알고리즘의 효율성이 모바일과 임베디드 컴퓨팅에서 유리하다는 점은 매우 중요하다. 깊은 네트워크 구조를 요구하는 이런 고려사항들이 정확도 수치보다 더 중요하다. 대부분의 실험에서 모델들은 mutiply-adds(곱하기와 더하기를 동시에 하는 연산)를 15억 회 이내로 수행하도록 설계되었다. 따라서 이들은 학문적 연구에 그치지 않고, 더 많은 데이터셋에 대해서도 합리적으로 실용화될 수 있다.
이 논문에서, 우리는 효율적이고 깊은 신경망 구조에 집중했다. 여기서 "deep"은 두 가지 의미로 사용되었다. 첫 번째로, 우리는 새로운 조직 수준인 "Inception module"을 도입한다. 두 번째로는 네트워크의 깊이가 증가한다는 직접적인 의미이다.
2. Related Work
LeNet-5을 시작으로, 합성곱 신경망(CNN)은 일반적으로 합성곱층이 쌓여있고 그 뒤에 전연결층이 따라붙는 표준적인 구조를 갖는다. 이 구조를 변형하는 것이 이미지 분류 논문들에서 유행이며, 변형된 구조는 MNIST, CIFAR, ImageNet 데이터셋에서 최고의 결과를 보였다. 이미지넷과 같은 큰 데이터셋에 대해서는 레이어의 수와 크기를 늘리면서 드롭아웃을 이용해 오버피팅을 방지하는 것이 최근 트렌드이다.
max-pooling 레이어가 공간 정보의 정확성을 잃어버릴 수 있지만, 합성곱 신경망 구조는 위치 파악, 물체 검출, 포즈 인식에서 좋은 성능을 보인다. Serre는 시각피질의 신경과학 모델에서 영감받아 서로 다른 크기의 필터를 사용했다. 인셉션 모델도 이와 비슷하지만, 인셉션 모듈이 수차례 반복되어 22층의 깊이를 갖는 다는 점과 인셉션 모델의 모든 커널이 학습된다는 점이 다르다.
Network-in-Network는 신경망의 표현력을 증가시키기 위해 제안되었다. 합성곱층에 적용될 때, 추가적인 1x1 합성곱층이 기존의 rectified linear activiation 뒤에 따른다. 1x1 합성곱층은 주로 계산 병목 현상을 줄이기 위해 차원을 줄이는 역할이다. 네트워크의 크기에 제한이 될 수 있는 현상을 방지함으로써 성능 감소 없이 네트워크의 폭과 깊이를 증가시킬 수 있다.
현재 물체 검출에 가장 좋은 성능을 보이는 것은 R-CNN이다. R-CNN은 전체 검출 과정을 두 가지 과정으로 나눴다. 우선 카테고리와 무관한 잠재적인 물체 제안을 위해 색깔이나 superpixel consistency과 같은 낮은 수준의 요소를 사용하고, 그 위치에서 물체 카테고리를 밝히기 위해 CNN 분류기를 사용한다. 우리는 검출 방식에서 이와 비슷한 접근법을 이용하지만, 두 단계 모두를 더 강화시켰다.
3. Motivation and High Level Considerations
신경망의 성능을 향상시키는 가장 좋은 방법은 크기를 늘리는 것이다. 이것은 레이어 수를 늘려 깊이를 늘리는 것과, 각 층에서 유닛의 수를 늘려 폭을 넓히는 두 가지 모두를 의미한다. 이것은 높은 품질의 모델을 교육하기 위한 간단하고 안전한 방법이며, 특히 많은 수의 데이터가 주어졌을 때 더 그렇다. 그러나 이런 간단한 방법은 주로 두 가지 단점이 있다.
큰 크기는 일반적으로 파라미터가 많다는 뜻이기 때문에 오버피팅의 가능성이 높고, 특히 트레이닝셋의 수가 제한되어 있을 때 더 그렇다. 질 좋은 데이터 셋을 만드는 것은 까다롭고 비용이 들기 때문에 이로 인한 병목 현상이 생길 수 있다.
또다른 단점은, 네트워크 크기를 균일하게 증가시키면, 계산량이 급격하게 올라간다는 점이다. 합성곱층의 크기를 두 배 키우면 계산량은 네 배만큼 올라간다. 만약 추가된 파라미터들이 0에 가까운 가중치로 학습된다면, 많은 수의 계산들은 버려지게 되어 비효율적이다. 계산능력은 제한적이기 때문에, 크기를 무분별하게 늘리는 것보다는 최대한 효율적인 파라미터 분포가 좋다.
이런 문제들을 해결하는 근본적인 방법은 전연결층을 부분적으로 연결된 구조로 바꾸는 것이며, 심지어 합성곱에서도 그렇다. 이 방법은 생체 시스템을 따라한다는 점뿐만 아니라, 확고한 이론적인 토대가 갖춰졌다는 이점이 있다. 만약 데이터셋의 확률적인 분포가 크고, sparse한 네트워크로 표현될 수 있다면, 마지막 레이어의 활성화 층의 상관 통계를 분석하고 높은 상관을 갖는 출력들의 뉴런을 모음으로써 레이어들을 쌓아 최적의 네트워크 구조를 만들 수 있다. 비록 엄밀한 수학적 증명은 강한 전제 조건을 필요로 하지만, 이런 성질이 Hebbian principle(함께 빛나는 뉴런들은 함께 묶여있다)과 같은 맥락이라는 것은 이들의 근본 원리를 가벼운 조건에서도 적용 가능하다는 것을 의미한다.
반대로, 최근 컴퓨터 구조는 non-uniform sparse data structure를 계산할 때 비효율적이다. 계산량이 100배나 줄었는데도 불구하고, lookup and cache miss에 드는 비용이 너무 커서 sparse matrix로 바꾸는 것이 효과가 없을 정도이다. CPU 또는 GPU의 세부사항들을 사용하면서 행렬 계산을 빠르게 할 수 있는, 꾸준히 발전하고 상당히 조정된 많은 수의 라이브러리들이 사용되고 있음에도 불구하고, 갭은 커졌다. 또한, non-uniform sparse 모델들은 정교한 공학과 컴퓨터 구조를 요구한다. 최근 비전 분야의 머신러닝 시스템들은 합성곱을 사용함으로써 공간 도메인의 희소성을 활용한다. 그러나, 합성곱은 앞쪽 레이어의 패치에 있는 밀도 높은 연결들의 집합처럼 구현된다. ConvNets는 대칭성을 없애고 학습을 향상시키기 위해 임의의, 희소한 연결을 특징 차원에 이용한다. 최근 트렌드는 병렬 컴퓨팅을 최적화하기 위해 다시 전연결을 하는 것으로 돌아가고 있다.
이러한 사실들이 다음 단계에 가능성이 있는지 질문을 이끌어냈다. 이론에서 제안된 것처럼 필터 수준에서 추가적인 희소성을 사용하는 구조. 희소 행렬 계산에 관한 많은 문헌들은 희소 행렬을 상대적으로 밀집된 하위행렬으로 모으는 것이 희소 행렬 곱셈에서 좋은 성능을 보이는 경향이 있다고 한다. 이와 비슷한 방법이 가까운 미래에 non-uniform 딥러닝 구조를 자동으로 구성하는데 사용될 것이라는 생각은 틀렸다고 보이지 않는다.
인셉션 구조는 정교한 신경망 구조 설계 알고리즘의 가상의 출력을 평가하기 위한 연구에서 시작되었다. 이것은 희소 구조를 근사하거나 쉽게 사용할 수 있는 요소들로부터 나오는 가상의 결과를 포함한다. 매우 위험한 작업이었음에도 불고하고, 두번의 반복 이후에 우리는 이미 이전 구조보다 더 나은 결과를 확인할 수 있었다. 학습률, 하이퍼파라미터를 조절하고, 학습 방법을 향상시키고 나서, 우리는 인셉션 구조가 localization과 물체 검출에 뛰어나다는 것을 알게 되었다. 흥미롭게도, 대부분의 모델들은 지역적으로는 최적화된 것으로 보였다.
그래도 신중해야 하는 것은, 비록 제안된 구조가 성공적이었지만, 그 구조를 만들게 된 원리가 그것의 성능에 기여했는지는 아직 의문이다. 확신하기 위해서는 철저한 분석과 검증이 더 필요하다.
4. Architectural Details
인셉션 구조의 주요 아이디어는 합성곱 신경망에서 최적의 local sparse structure가 이미 이용가능한 dense components로 어떻게 근사될 수 있는지 알아내는 것이다. 우리가 필요한 것은 최적의 local structure를 찾아내고 그것을 공간적으로 반복하는 것이다.
이러한 인셉션 모듈이 서로의 위에 쌓여있기 때문에, 그들의 output correlation statistics는 다양하다. 고도로 추상화된 특징이 높이 있는 레이어에 의해 묘사될 때, 그들의 공간 집중도가 감소할 것으로 예상되는 것은 3x3 또는 5x5 합성곱층이 위로 갈수록 더 많아져야 한다는것을 의미한다.
위의 모듈을 사용했을 때 생기는 큰 문제중 하나는, 가장 위쪽 레이어에는 필터 수가 많아서 5x5 합성곱층은 비용이 엄청나게 비쌀 수도 있다. 이 문제는 풀링층이 더해졌을 때 더 명백해진다. 그들의 출력 필터 숫자는 이전 단계에서의 필터 숫자와 같다. 풀링 레이어의 출력을 합성곱층의 출력과 합치는 것은 단계에서 다른 단계로 넘어갈때 출력의 숫자가 커지는 것을 피할 수 없다. 심지어 이런 구조가 최적의 희소 구조를 만족할지라도, 이것은 비효율적이며 몇 단계만으로 계산량이 폭발할 수 있다.
이런 문제는 이 구조의 두번째 아이디어를 이끌어 냈다. 계산량이 너무 많이 늘어나는 곳에서 차원 축소과 투영을 신중하게 적용했다. 이것은 임베딩의 성공에 기인한다. 심지어 낮은 차원 임베딩이 상대적으로 큰 이미지 패치에 대해 많은 정보를 포함한다. 그러나, 임베딩은 밀집되고 압축된 형태의 정보를 표현하고, 압축된 정보는 모델링하기 더 어렵다. 우리는 대부분 장소에서 표현을 희소하게 유지하고 전체적으로 집계할 때마다 신호를 압축하고 싶다. 즉, 비용이 큰 3x3 및 5x5 합성곱 이전에 1x1 합성곱을 사용해 계산량을 줄인다. 축소를 위해 이용되는 것 외에도, ReLu를 사용하여 두 가지 목적으로 사용한다.
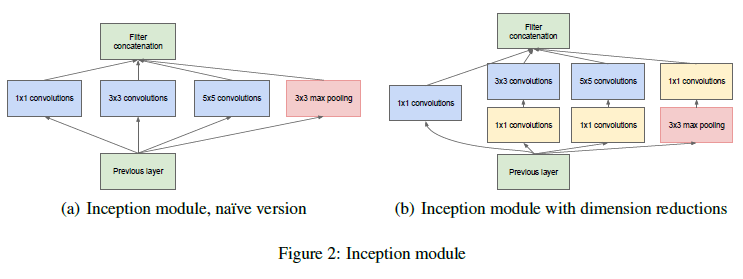
일반적으로, 인셉션 네트워크는 위의 모듈들이 max-pooling 레이어들과 함께 쌓여서 구성된다. 메모리 효율을 위한 기술적인 이유로, 높은 계층에서만 인셉션 모듈을 사용하기 시작하는게 이득이다. 낮은 게층에서는 전통적인 합성곱신경층을 사용한다. 이것은 꼭 필요한 것은 아니지만, 모델의 실행에서 비효율적인 부분을 반영하였다.
이 구조의 가장 이득인 부분은, 각 단계에서 레이어의 수를 늘려도 계산 복잡도가 폭발적으로 늘어나지 않는다는 것이다. 어디에서나 사용가능한 차원 축소는 많은 수의 입력 필터 수를 보호해주는데, 큰 패치 사이즈로 합성곱을 진행하기 전에 차원을 축소한다. 다른 실용적인 특성은, 시각 정보가 다양한 스케일로 처리된 다음 집계되어 다음 단계에서 다른 스케일의 피처로 추상화 할 수 있다는 직관과 일치한다는 점이다.
5. GoogLeNet


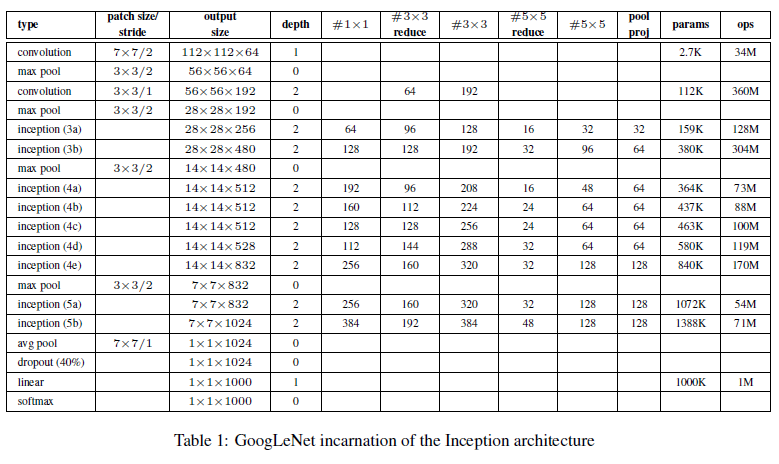
모든 합성곱층은 ReLU를 사용했다. 입력 샘플의 크기는 [224, 224, 3]이고, 평균값을 빼줬다. “#3x3 reduce” 와 “#5x5 reduce"는 차원 축소 레이어의 1x1 필터의 수이다. pool proj colum의 max-pooling 다음에 오는 투영 레이어의 1x1 필터를 볼 수 있다. 이런 모든 차원 축소 / 투영 레이어들 역시 ReLU를 사용한다.
네트워크는 계산 효율성과 실용성을 염두하고 설계되었다. 따라서 추론은 제한된 계산 능력을 갖는 기기에서도 가능하다. 네트워크에서 파라미터를 갖는 레이어는 22개이고, 전체 레이어는 100개 정도 된다. 그러나 이 숫자는 사용된 기계학습 인프라시스템에 따라 다르다.
주어진 네트워크가 상당히 깊을 때, 기울기의 역전파를 효과적인 방법으로 모든 레이어에 전파하는 방법이 문제였다. 한가지 흥미로운 점은, 비교적 얕은 네트워크의 높은 성능은 네트워크 중심부에 있는 레이어에서 만들어진 피처들이 구분 가능성이 높야 한다는 점을 의미한다. 중간 레이어에 보조 분류기를 추가로 연결함으로써, 우리는 낮은 단계에서 구분할 수 있게 하는 것, 역전파 기울기 값을 증가하는 것, 추가적인 정규화를 제공하는 것을 기대할 수 있다. 학습 과정에서, 이들의 로스는 0.3의 가중치가 곱해진 채 전체 가중치에 더해진다.
6. Training Methodology
우리는 asynchronous SGD를 0.9 모멘텀으로 사용했고, 학습률을 9에폭마다 4%씩 감소시켰다. 이미지를 다양한 크기로 자르고, 종횡비를 랜덤하게 변형시키는 것은 오버피팅을 방지하는데 효과가 있었다. 게다가, 우리는 보강법을 다양하게 사용했다. 따라서 어떤 요소가 성능을 향상시켰다고 명확하게 말하기 어렵다.
7. ILSVRC 2014 Classification Callenge Setup and Results
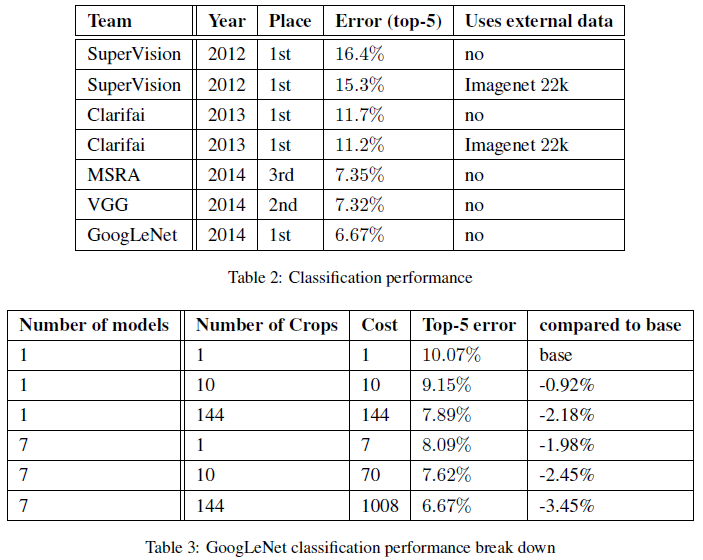
8. ILSVRC 2014 Detection Callenge Setup and Results
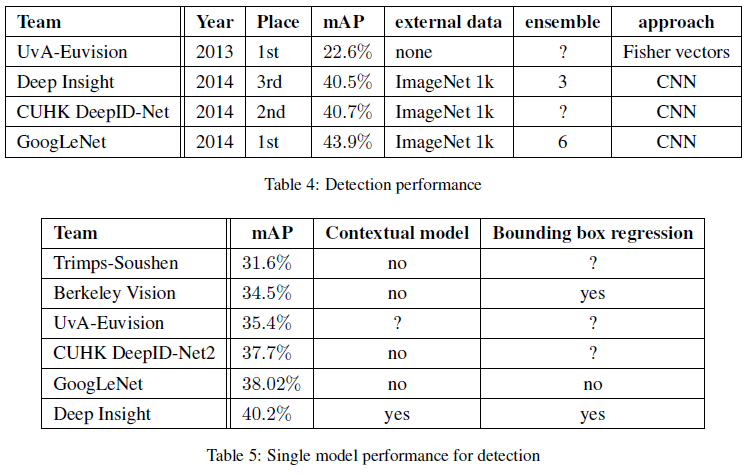
9. Conclusions
dense building block으로 expected optimal sparse structure을 근사하는 것이 신경망을 향상시키기 위해 사용 가능한 방법이라는 것을 우리의 결과가 증명하는 것으로 보인다. 이런 방식의 가장 큰 장점은, 적당한 계산 능력을 요구하면서 상당한 성능 향상을 얻을 수 있다는 점이다. 우리 방법은 희소 구조를 이용하는 것이 현실성 있고 일반적으로 사용할만한 아이디어라는 점이 중요하다.
10. Acknowledgements
'Deep Learning > CNN Models' 카테고리의 다른 글
| Resnet (2015) (0) | 2019.11.05 |
|---|---|
| AlexNet (2012) (0) | 2019.10.26 |
| Checklist (0) | 2019.10.26 |

